Speeding up rxode2

A note about the speed of the functional form for rxode2

The functional form has the benefit that it is what is supported by nlmixr2 and therefore there is only one interface between solving and estimating, and it takes some computation time to get to the underlying “classic” simulation code.

These models are in the form of:

library(rxode2)
#> rxode2 5.0.1.9000 using 2 threads (see ?getRxThreads)
#>   no cache: create with `rxCreateCache()`

mod1 <- function() {
  ini({
    KA   <- 0.3
    CL   <- 7
    V2   <- 40
    Q    <- 10
    V3   <- 300
    Kin  <- 0.2
    Kout <- 0.2
    EC50 <- 8
  })
  model({
    C2 = centr/V2
    C3 = peri/V3
    d/dt(depot) = -KA*depot
    d/dt(centr) = KA*depot - CL*C2 - Q*C2 + Q*C3
    d/dt(peri) = Q*C2 - Q*C3
    d/dt(eff) = Kin - Kout*(1-C2/(EC50+C2))*eff
    eff(0) = 1
  })
}

Or you can also specify the end-points for simulation/estimation just like nlmixr2:

mod2f <- function() {
  ini({
    TKA   <- 0.3
    TCL   <- 7
    TV2   <- 40
    TQ    <- 10
    TV3   <- 300
    TKin  <- 0.2
    TKout <- 0.2
    TEC50 <- 8
    eta.cl + eta.v ~ c(0.09,
                       0.08, 0.25)
    c2.prop.sd <- 0.1
    eff.add.sd <- 0.1
  })
  model({
    KA <- TKA
    CL <- TCL*exp(eta.cl)
    V2  <- TV2*exp(eta.v)
    Q   <- TQ
    V3  <- TV3
    Kin  <- TKin
    Kout <- TKout
    EC50 <- TEC50
    C2 = centr/V2
    C3 = peri/V3
    d/dt(depot) = -KA*depot
    d/dt(centr) = KA*depot - CL*C2 - Q*C2 + Q*C3
    d/dt(peri) = Q*C2 - Q*C3
    d/dt(eff) = Kin - Kout*(1-C2/(EC50+C2))*eff
    eff(0) = 1
    C2 ~ prop(c2.prop.sd)
    eff ~ add(eff.add.sd)
  })
}

For every solve, there is a compile (or a cached compile) of the underlying model. If you wish to speed this process up you can use the two underlying rxode2 classic models. This takes two steps:

Parsing/evaluating the model
Creating the simulation model

The first step can be done by rxode2(mod1) or mod1() (or for the second model too).

mod1 <- mod1()
mod2f <- rxode2(mod2f)
#> ℹ parameter labels from comments are typically ignored in non-interactive mode
#> ℹ Need to run with the source intact to parse comments

The second step is to create the underlying “classic” rxode2 model, which can be done with two different methods:$simulationModel and $simulationIniModel. The $simulationModel will provide the simulation code without the initial conditions pre-pended, the $simulationIniModel will pre-pend the values. When the endpoints are specified, the simulation code for each endpoint is also output. You can see the differences below:

summary(mod1$simulationModel)
#> rxode2 5.0.1.9000 model named rx_6b88daee2c86796db0a6ac0ef36e32b2 model (✔ ready). 
#> DLL: /tmp/RtmpPwyVXB/rxode2/rx_6b88daee2c86796db0a6ac0ef36e32b2__.rxd/rx_6b88daee2c86796db0a6ac0ef36e32b2_.so
#> NULL
#> 
#> Calculated Variables:
#> [1] "C2" "C3"
#> ── rxode2 Model Syntax ──
#> rxode2({
#>     param(KA, CL, V2, Q, V3, Kin, Kout, EC50)
#>     C2 = centr/V2
#>     C3 = peri/V3
#>     d/dt(depot) = -KA * depot
#>     d/dt(centr) = KA * depot - CL * C2 - Q * C2 + Q * C3
#>     d/dt(peri) = Q * C2 - Q * C3
#>     d/dt(eff) = Kin - Kout * (1 - C2/(EC50 + C2)) * eff
#>     eff(0) = 1
#> })
summary(mod1$simulationIniModel)
#> rxode2 5.0.1.9000 model named rx_52af5bbe499530a8f436378ded51fa34 model (✔ ready). 
#> DLL: /tmp/RtmpPwyVXB/rxode2/rx_52af5bbe499530a8f436378ded51fa34__.rxd/rx_52af5bbe499530a8f436378ded51fa34_.so
#> NULL
#> 
#> Calculated Variables:
#> [1] "C2" "C3"
#> ── rxode2 Model Syntax ──
#> rxode2({
#>     param(KA, CL, V2, Q, V3, Kin, Kout, EC50)
#>     KA = 0.3
#>     CL = 7
#>     V2 = 40
#>     Q = 10
#>     V3 = 300
#>     Kin = 0.2
#>     Kout = 0.2
#>     EC50 = 8
#>     C2 = centr/V2
#>     C3 = peri/V3
#>     d/dt(depot) = -KA * depot
#>     d/dt(centr) = KA * depot - CL * C2 - Q * C2 + Q * C3
#>     d/dt(peri) = Q * C2 - Q * C3
#>     d/dt(eff) = Kin - Kout * (1 - C2/(EC50 + C2)) * eff
#>     eff(0) = 1
#> })
summary(mod2f$simulationModel)
#> rxode2 5.0.1.9000 model named rx_cefee9dd1d1d00110358670e760f5e7f model (✔ ready). 
#> DLL: /tmp/RtmpPwyVXB/rxode2/rx_cefee9dd1d1d00110358670e760f5e7f__.rxd/rx_cefee9dd1d1d00110358670e760f5e7f_.so
#> NULL
#> 
#> Calculated Variables:
#>  [1] "KA"       "CL"       "V2"       "Q"        "V3"       "Kin"     
#>  [7] "Kout"     "EC50"     "C2"       "C3"       "ipredSim" "sim"     
#> ── rxode2 Model Syntax ──
#> rxode2({
#>     param(TKA, TCL, TV2, TQ, TV3, TKin, TKout, TEC50, c2.prop.sd, 
#>         eff.add.sd, eta.cl, eta.v)
#>     KA = TKA
#>     CL = TCL * exp(eta.cl)
#>     V2 = TV2 * exp(eta.v)
#>     Q = TQ
#>     V3 = TV3
#>     Kin = TKin
#>     Kout = TKout
#>     EC50 = TEC50
#>     C2 = centr/V2
#>     C3 = peri/V3
#>     d/dt(depot) = -KA * depot
#>     d/dt(centr) = KA * depot - CL * C2 - Q * C2 + Q * C3
#>     d/dt(peri) = Q * C2 - Q * C3
#>     d/dt(eff) = Kin - Kout * (1 - C2/(EC50 + C2)) * eff
#>     eff(0) = 1
#>     if (CMT == 5) {
#>         rx_yj_ ~ 2
#>         rx_lambda_ ~ 1
#>         rx_low_ ~ 0
#>         rx_hi_ ~ 1
#>         rx_pred_f_ ~ C2
#>         rx_pred_ ~ rx_pred_f_
#>         rx_r_ ~ (rx_pred_f_ * c2.prop.sd)^2
#>         ipredSim = rxTBSi(rx_pred_, rx_lambda_, rx_yj_, rx_low_, 
#>             rx_hi_)
#>         sim = rxTBSi(rx_pred_ + sqrt(rx_r_) * rxerr.C2, rx_lambda_, 
#>             rx_yj_, rx_low_, rx_hi_)
#>     }
#>     if (CMT == 4) {
#>         rx_yj_ ~ 2
#>         rx_lambda_ ~ 1
#>         rx_low_ ~ 0
#>         rx_hi_ ~ 1
#>         rx_pred_f_ ~ eff
#>         rx_pred_ ~ rx_pred_f_
#>         rx_r_ ~ (eff.add.sd)^2
#>         ipredSim = rxTBSi(rx_pred_, rx_lambda_, rx_yj_, rx_low_, 
#>             rx_hi_)
#>         sim = rxTBSi(rx_pred_ + sqrt(rx_r_) * rxerr.eff, rx_lambda_, 
#>             rx_yj_, rx_low_, rx_hi_)
#>     }
#>     cmt(C2)
#>     dvid(5, 4)
#> })
summary(mod2f$simulationIniModel)
#> rxode2 5.0.1.9000 model named rx_486aa95cd36631129203c1d6056b2317 model (✔ ready). 
#> DLL: /tmp/RtmpPwyVXB/rxode2/rx_486aa95cd36631129203c1d6056b2317__.rxd/rx_486aa95cd36631129203c1d6056b2317_.so
#> NULL
#> 
#> Calculated Variables:
#>  [1] "KA"       "CL"       "V2"       "Q"        "V3"       "Kin"     
#>  [7] "Kout"     "EC50"     "C2"       "C3"       "ipredSim" "sim"     
#> ── rxode2 Model Syntax ──
#> rxode2({
#>     param(TKA, TCL, TV2, TQ, TV3, TKin, TKout, TEC50, c2.prop.sd, 
#>         eff.add.sd, eta.cl, eta.v)
#>     rxerr.C2 = 1
#>     rxerr.eff = 1
#>     TKA = 0.3
#>     TCL = 7
#>     TV2 = 40
#>     TQ = 10
#>     TV3 = 300
#>     TKin = 0.2
#>     TKout = 0.2
#>     TEC50 = 8
#>     c2.prop.sd = 0.1
#>     eff.add.sd = 0.1
#>     eta.cl = 0
#>     eta.v = 0
#>     KA = TKA
#>     CL = TCL * exp(eta.cl)
#>     V2 = TV2 * exp(eta.v)
#>     Q = TQ
#>     V3 = TV3
#>     Kin = TKin
#>     Kout = TKout
#>     EC50 = TEC50
#>     C2 = centr/V2
#>     C3 = peri/V3
#>     d/dt(depot) = -KA * depot
#>     d/dt(centr) = KA * depot - CL * C2 - Q * C2 + Q * C3
#>     d/dt(peri) = Q * C2 - Q * C3
#>     d/dt(eff) = Kin - Kout * (1 - C2/(EC50 + C2)) * eff
#>     eff(0) = 1
#>     if (CMT == 5) {
#>         rx_yj_ ~ 2
#>         rx_lambda_ ~ 1
#>         rx_low_ ~ 0
#>         rx_hi_ ~ 1
#>         rx_pred_f_ ~ C2
#>         rx_pred_ ~ rx_pred_f_
#>         rx_r_ ~ (rx_pred_f_ * c2.prop.sd)^2
#>         ipredSim = rxTBSi(rx_pred_, rx_lambda_, rx_yj_, rx_low_, 
#>             rx_hi_)
#>         sim = rxTBSi(rx_pred_ + sqrt(rx_r_) * rxerr.C2, rx_lambda_, 
#>             rx_yj_, rx_low_, rx_hi_)
#>     }
#>     if (CMT == 4) {
#>         rx_yj_ ~ 2
#>         rx_lambda_ ~ 1
#>         rx_low_ ~ 0
#>         rx_hi_ ~ 1
#>         rx_pred_f_ ~ eff
#>         rx_pred_ ~ rx_pred_f_
#>         rx_r_ ~ (eff.add.sd)^2
#>         ipredSim = rxTBSi(rx_pred_, rx_lambda_, rx_yj_, rx_low_, 
#>             rx_hi_)
#>         sim = rxTBSi(rx_pred_ + sqrt(rx_r_) * rxerr.eff, rx_lambda_, 
#>             rx_yj_, rx_low_, rx_hi_)
#>     }
#>     cmt(C2)
#>     dvid(5, 4)
#> })

If you wish to speed up multiple simualtions from the rxode2 functions, you need to pre-calculate care of the steps above:

mod1 <- mod1$simulationModel

mod2 <- mod2f$simulationModel

These functions then can act like a normal ui model to be solved. You can convert them back to a UI as.rxUi() or a function as.function() as needed.

To increase speed for multiple simulations from the same model you should use the lower level simulation model (ie $simulationModel or $simulationIniModel depending on what you need)

Increasing rxode2 speed by multi-subject parallel solving

Using the classic rxode2 model specification (which we can convert from a functional/ui model style) we will continue the discussion on rxode2 speed enhancements.

rxode2 originally developed as an ODE solver that allowed an ODE solve for a single subject. This flexibility is still supported.

The original code from the rxode2 tutorial is below:

library(rxode2)

library(microbenchmark)
library(ggplot2)

mod1 <- rxode2({
    C2 = centr/V2
    C3 = peri/V3
    d/dt(depot) = -KA*depot
    d/dt(centr) = KA*depot - CL*C2 - Q*C2 + Q*C3
    d/dt(peri) = Q*C2 - Q*C3
    d/dt(eff) = Kin - Kout*(1-C2/(EC50+C2))*eff
    eff(0) = 1
})

## Create an event table

ev <- et() |>
    et(amt=10000, addl=9,ii=12) |>
    et(time=120, amt=20000, addl=4, ii=24) |>
    et(0:240) ## Add Sampling

nsub <- 100 # 100 sub-problems
sigma <- matrix(c(0.09,0.08,0.08,0.25),2,2) # IIV covariance matrix
mv <- rxRmvn(n=nsub, rep(0,2), sigma) # Sample from covariance matrix
CL <- 7*exp(mv[,1])
V2 <- 40*exp(mv[,2])
params.all <- cbind(KA=0.3, CL=CL, V2=V2, Q=10, V3=300,
                    Kin=0.2, Kout=0.2, EC50=8)

For Loop

The slowest way to code this is to use a for loop. In this example we will enclose it in a function to compare timing.

runFor <- function(){
    res <- NULL
    for (i in 1:nsub) {
        params <- params.all[i,]
        x <- mod1$solve(params, ev)
        ##Store results for effect compartment
        res <- cbind(res, x[, "eff"])
    }
    return(res)
}

Running with apply

In general for R, the apply types of functions perform better than a for loop, so the tutorial also suggests this speed enhancement

runSapply <- function(){
    res <- apply(params.all, 1, function(theta)
        mod1$run(theta, ev)[, "eff"])
}

Run using a single-threaded solve

You can also have rxode2 solve all the subject simultaneously without collecting the results in R, using a single threaded solve.

The data output is slightly different here, but still gives the same information:

runSingleThread <- function(){
  solve(mod1, params.all, ev, cores=1)[,c("sim.id", "time", "eff")]
}

Run a 2 threaded solve

rxode2 supports multi-threaded solves, so another option is to have 2 threads (called cores in the solve options, you can see the options in rxControl() or rxSolve()).

run2Thread <- function(){
  solve(mod1, params.all, ev, cores=2)[,c("sim.id", "time", "eff")]
}

Compare the times between all the methods

Now the moment of truth, the timings:

bench <- microbenchmark(runFor(), runSapply(), runSingleThread(),run2Thread())
print(bench)
#> Unit: milliseconds
#>               expr       min        lq      mean    median        uq       max
#>           runFor() 431.70538 439.73340 448.42457 443.13075 450.56665 613.67939
#>        runSapply() 435.41924 442.87541 450.44197 446.44560 452.10931 598.04298
#>  runSingleThread()  37.93731  38.13860  38.90400  38.35138  38.67753  48.06136
#>       run2Thread()  24.60569  24.96795  25.79628  25.45749  26.17723  34.81978
#>  neval
#>    100
#>    100
#>    100
#>    100

autoplot(bench)
#> Warning: `aes_string()` was deprecated in ggplot2 3.0.0.
#> ℹ Please use tidy evaluation idioms with `aes()`.
#> ℹ See also `vignette("ggplot2-in-packages")` for more information.
#> ℹ The deprecated feature was likely used in the microbenchmark package.
#>   Please report the issue at
#>   <https://github.com/joshuaulrich/microbenchmark/issues/>.
#> This warning is displayed once per session.
#> Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
#> generated.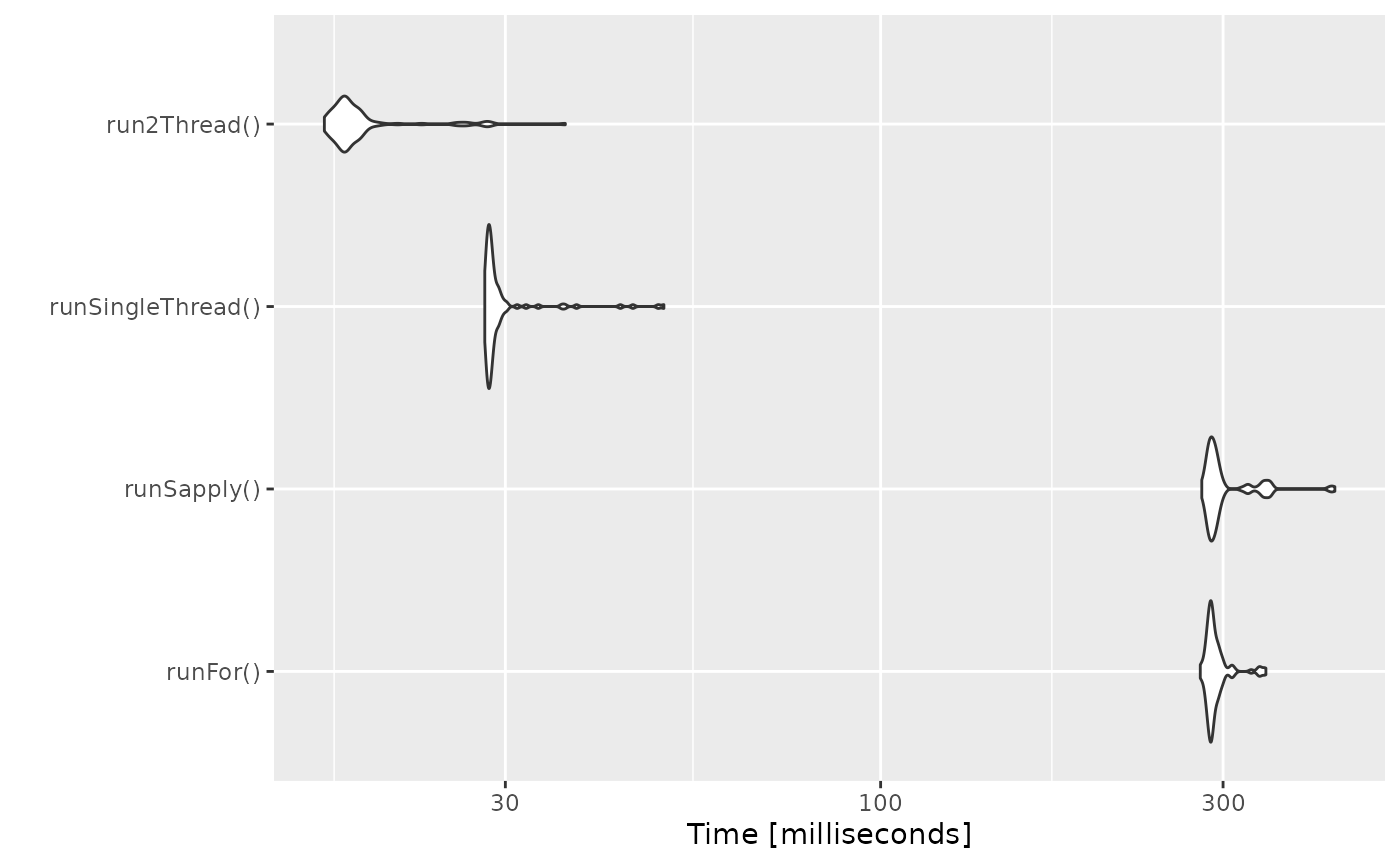

It is clear that the largest jump in performance when using the solve method and providing all the parameters to rxode2 to solve without looping over each subject with either a for or a sapply. The number of cores/threads applied to the solve also plays a role in the solving.

We can explore the number of threads further with the following code:

runThread <- function(n){
    solve(mod1, params.all, ev, cores=n)[,c("sim.id", "time", "eff")]
}

bench <- eval(parse(text=sprintf("microbenchmark(%s)",
                                     paste(paste0("runThread(", seq(1, 2 * rxCores()),")"),
                                           collapse=","))))
print(bench)
#> Unit: milliseconds
#>          expr      min       lq     mean   median       uq      max neval
#>  runThread(1) 38.07084 38.29567 39.27086 38.47865 38.71008 51.01061   100
#>  runThread(2) 24.63511 25.01095 26.89674 25.37648 26.42383 37.41820   100
#>  runThread(3) 26.05490 26.39605 27.89702 26.75942 29.88481 35.23709   100
#>  runThread(4) 25.74680 25.93178 26.76573 26.11195 26.36923 35.37682   100

autoplot(bench)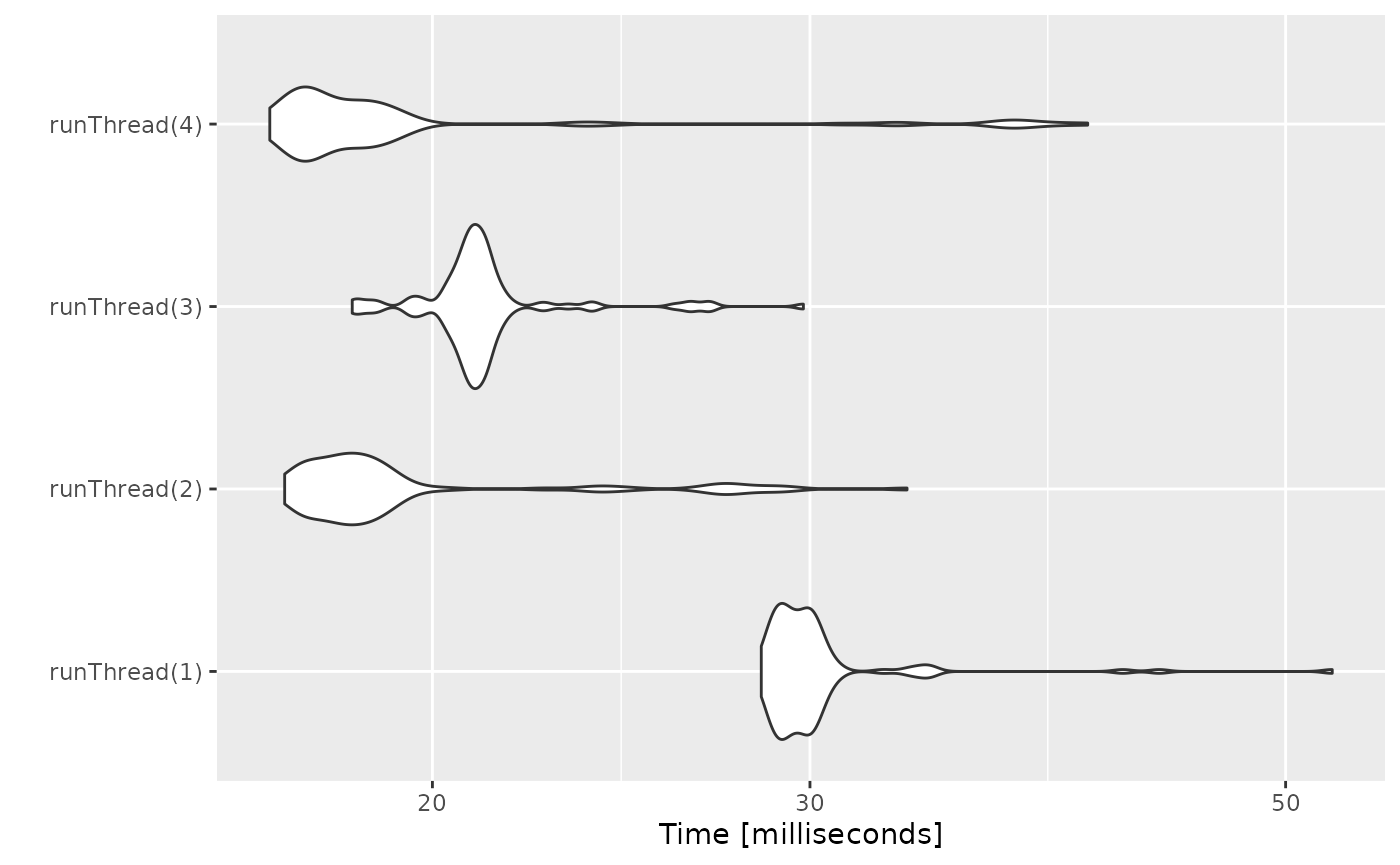

There can be a suite spot in speed vs number or cores. The system type (mac, linux, windows and/or processor), complexity of the ODE solving and the number of subjects may affect this arbitrary number of threads. 4 threads is a good number to use without any prior knowledge because most systems these days have at least 4 threads (or 2 processors with 4 threads).

Increasing speed with compiler options

One of the way that allows faster ODE solving is to make some approximations that make some math operators like exp() faster but not technically accurate enough to follow the IEEE standard for the math functions values (there are other implications that I will not cover here).

While these are optimizations are opt-in for Julia since they compile everything each session, CRAN has a more conservative approach since individuals do not compile each R function before running it.

Still, rxode2 models can be compiled with this option without disturbing CRAN policies. The key is to set an option. Here is an example:

# Using the first example subset to PK
mod2f <- function() {
  ini({
    TKA   <- 0.3
    TCL   <- 7
    TV2   <- 40
    TQ    <- 10
    TV3   <- 300
    TKin  <- 0.2
    TKout <- 0.2
    TEC50 <- 8
    eta.cl + eta.v ~ c(0.09,
                       0.08, 0.25)
    c2.prop.sd <- 0.1
  })
  model({
    KA <- TKA
    CL <- TCL*exp(eta.cl)
    V2  <- TV2*exp(eta.v)
    Q   <- TQ
    V3  <- TV3
    Kin  <- TKin
    Kout <- TKout
    EC50 <- TEC50
    C2 = centr/V2
    C3 = peri/V3
    d/dt(depot) = -KA*depot
    d/dt(centr) = KA*depot - CL*C2 - Q*C2 + Q*C3
    d/dt(peri) = Q*C2 - Q*C3
    C2 ~ prop(c2.prop.sd)
  })
}

mod2f <- mod2f()

mod2s <- mod2f$simulationIniModel

ev  <- et(amountUnits="mg", timeUnits="hours") |>
  et(amt=10000, addl=9,ii=12,cmt="depot") |>
  et(time=120, amt=2000, addl=4, ii=14, cmt="depot") |>
  et(0:240) # Add sampling

bench1 <- microbenchmark(standardCompile=rxSolve(mod2s, ev, nSub=1000))

# Now clear the cache of models so we can change the compile options for the same model
rxClean()

# Use withr to preserve the options
withr::with_options(list(rxode2.compile.O="fast"), {
  mod2s <- mod2f$simulationIniModel
})

bench2 <- microbenchmark(fastCompile=rxSolve(mod2s, ev, nSub=1000))

bench <- rbind(bench1, bench2)

print(bench)
#> Unit: milliseconds
#>             expr      min       lq     mean  median       uq      max neval
#>  standardCompile 428.6039 440.4376 494.8996 450.733 619.4960 649.2600   100
#>      fastCompile 428.8426 440.2540 496.2292 451.589 613.5712 661.5824   100

autoplot(bench)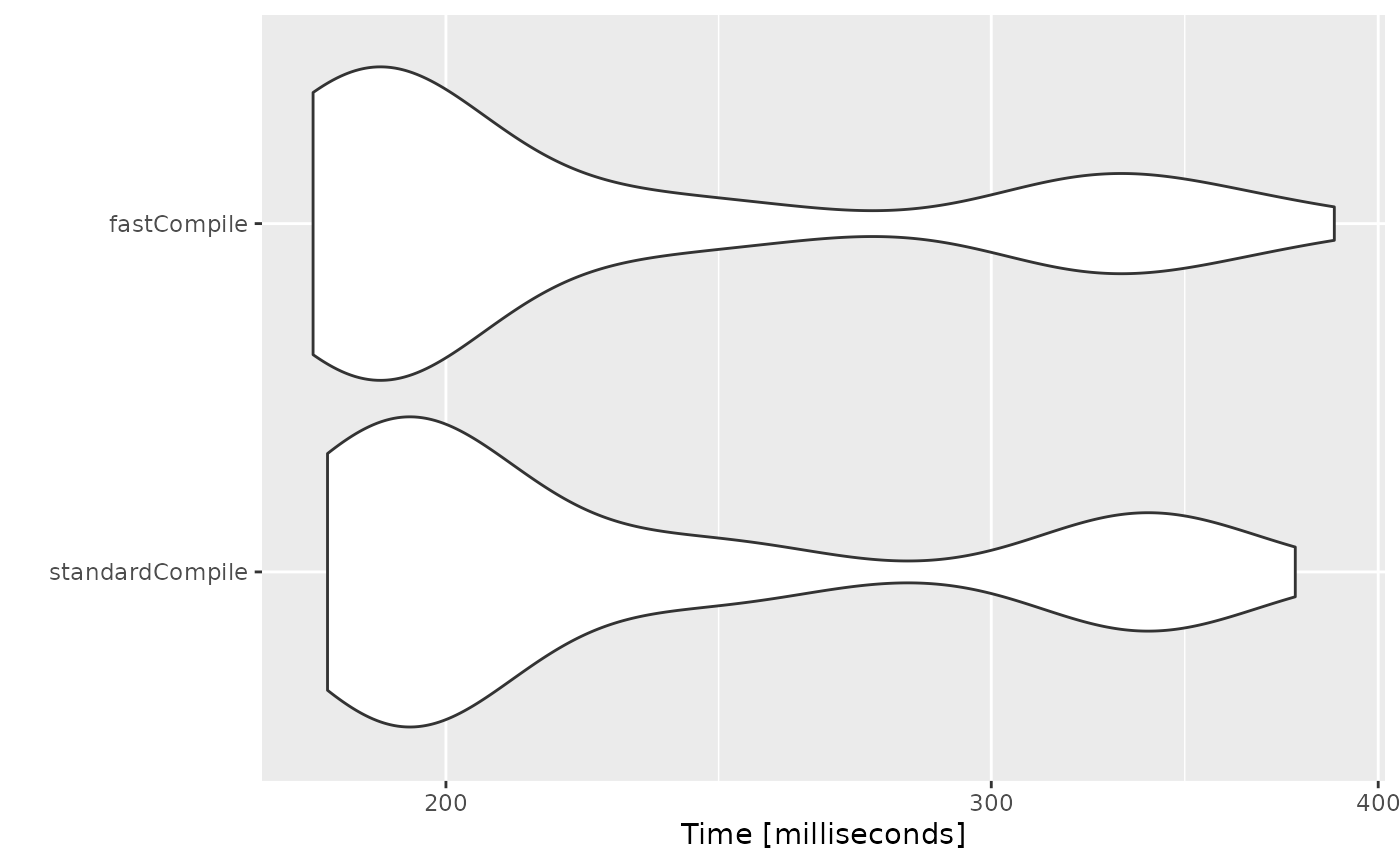

Note compiler settings can be tricky and if you setup your system wide Makevars it may interact with this setting. For example if you use ccache the compile may not be produced with the same options since it was cached with the other options.

For example, on the github runner (which generates this page), there is no advantage to the "fast" compile. However, on my development laptop there is some minimal speed increase. You should probably check before using this yourself.

This is disabled by default since there is only minimum increase in speed.

A real life example

cBefore some of the parallel solving was implemented, the fastest way to run rxode2 was with lapply. This is how Rik Schoemaker created the data-set for nlmixr comparisons, but reduced to run faster automatic building of the pkgdown website.

library(rxode2)
library(data.table)
#Define the rxode2 model
  ode1 <- "
  d/dt(abs)    = -KA*abs;
  d/dt(centr)  =  KA*abs-(CL/V)*centr;
  C2=centr/V;
  "

#Create the rxode2 simulation object
mod1 <- rxode2(model = ode1)

#Population parameter values on log-scale
  paramsl <- c(CL = log(4),
               V = log(70),
               KA = log(1))
#make 10,000 subjects to sample from:
  nsubg <- 300 # subjects per dose
  doses <- c(10, 30, 60, 120)
  nsub <- nsubg * length(doses)
#IIV of 30% for each parameter
  omega <- diag(c(0.09, 0.09, 0.09))# IIV covariance matrix
  sigma <- 0.2
#Sample from the multivariate normal
  set.seed(98176247)
  rxSetSeed(98176247)
  library(MASS)
  mv <-
    mvrnorm(nsub, rep(0, dim(omega)[1]), omega) # Sample from covariance matrix
#Combine population parameters with IIV
  params.all <-
    data.table(
      "ID" = seq(1:nsub),
      "CL" = exp(paramsl['CL'] + mv[, 1]),
      "V" = exp(paramsl['V'] + mv[, 2]),
      "KA" = exp(paramsl['KA'] + mv[, 3])
    )
#set the doses (looping through the 4 doses)
params.all[, AMT := rep(100 * doses,nsubg)]

Startlapply <- Sys.time()

#Run the simulations using lapply for speed
  s = lapply(1:nsub, function(i) {
#selects the parameters associated with the subject to be simulated
    params <- params.all[i]
#creates an eventTable with 7 doses every 24 hours
    ev <- eventTable()
    ev$add.dosing(
      dose = params$AMT,
      nbr.doses = 1,
      dosing.to = 1,
      rate = NULL,
      start.time = 0
    )
#generates 4 random samples in a 24 hour period
    ev$add.sampling(c(0, sort(round(sample(runif(600, 0, 1440), 4) / 60, 2))))
#runs the rxode2 simulation
    x <- as.data.table(mod1$run(params, ev))
#merges the parameters and ID number to the simulation output
    x[, names(params) := params]
  })

#runs the entire sequence of 100 subjects and binds the results to the object res
  res = as.data.table(do.call("rbind", s))

Stoplapply <- Sys.time()

print(Stoplapply - Startlapply)
#> Time difference of 28.65077 secs

By applying some of the new parallel solving concepts you can simply run the same simulation both with less code and faster:

rx <- rxode2({
    CL =  log(4)
    V = log(70)
    KA = log(1)
    CL = exp(CL + eta.CL)
    V = exp(V + eta.V)
    KA = exp(KA + eta.KA)
    d/dt(abs)    = -KA*abs;
    d/dt(centr)  =  KA*abs-(CL/V)*centr;
    C2=centr/V;
})

omega <- lotri(eta.CL ~ 0.09,
               eta.V ~ 0.09,
               eta.KA ~ 0.09)

doses <- c(10, 30, 60, 120)


startParallel <- Sys.time()
ev <- do.call("rbind",
        lapply(seq_along(doses), function(i){
            et() |>
                et(amt=doses[i]) |> # Add single dose
                et(0) |> # Add 0 observation
                ## Generate 4 samples in 24 hour period
                et(lapply(1:4, function(...){c(0, 24)})) |>
                et(id=seq(1, nsubg) + (i - 1) * nsubg) |>
                ## Convert to data frame to skip sorting the data
                ## When binding the data together
                as.data.frame()
        }))
## To better compare, use the same output, that is data.table
res <- rxSolve(rx, ev, omega=omega, returnType="data.table")
endParallel <- Sys.time()
print(endParallel - startParallel)
#> Time difference of 1.167356 secs

You can see a striking time difference between the two methods; A few things to keep in mind:

rxode2 use the thread-safe sitmo threefry routines for simulation of eta values. Therefore the results are expected to be different (also the random samples are taken in a different order which would be different)
This prior simulation was run in R 3.5, which has a different random number generator so the results in this simulation will be different from the actual nlmixr comparison when using the slower simulation.
This speed comparison used data.table. rxode2 uses data.table internally (when available) try to speed up sorting, so this would be different than installations where data.table is not installed. You can force rxode2 to use order() when sorting by using forderForceBase(TRUE). In this case there is little difference between the two, though in other examples data.table’s presence leads to a speed increase (and less likely it could lead to a slowdown).

Want more ways to run multi-subject simulations

The version since the tutorial has even more ways to run multi-subject simulations, including adding variability in sampling and dosing times with et() (see rxode2 events for more information), ability to supply both an omega and sigma matrix as well as adding as a thetaMat to R to simulate with uncertainty in the omega, sigma and theta matrices; see rxode2 simulation vignette.

Session Information

The session information:

sessionInfo()
#> R version 4.5.2 (2025-10-31)
#> Platform: x86_64-pc-linux-gnu
#> Running under: Ubuntu 24.04.3 LTS
#> 
#> Matrix products: default
#> BLAS:   /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3 
#> LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.26.so;  LAPACK version 3.12.0
#> 
#> locale:
#>  [1] LC_CTYPE=C.UTF-8       LC_NUMERIC=C           LC_TIME=C.UTF-8       
#>  [4] LC_COLLATE=C.UTF-8     LC_MONETARY=C.UTF-8    LC_MESSAGES=C.UTF-8   
#>  [7] LC_PAPER=C.UTF-8       LC_NAME=C              LC_ADDRESS=C          
#> [10] LC_TELEPHONE=C         LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C   
#> 
#> time zone: UTC
#> tzcode source: system (glibc)
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#> [1] MASS_7.3-65          data.table_1.18.0    ggplot2_4.0.1       
#> [4] microbenchmark_1.5.0 rxode2_5.0.1.9000   
#> 
#> loaded via a namespace (and not attached):
#>  [1] sass_0.4.10           generics_0.1.4        lattice_0.22-7       
#>  [4] digest_0.6.39         magrittr_2.0.4        evaluate_1.0.5       
#>  [7] grid_4.5.2            RColorBrewer_1.1-3    fastmap_1.2.0        
#> [10] lotri_1.0.3           qs2_0.1.7             jsonlite_2.0.0       
#> [13] rxode2ll_2.0.13       backports_1.5.0       scales_1.4.0         
#> [16] lazyeval_0.2.2        textshaping_1.0.4     jquerylib_0.1.4      
#> [19] cli_3.6.5             symengine_0.2.10      crayon_1.5.3         
#> [22] rlang_1.1.7           units_1.0-0           withr_3.0.2          
#> [25] cachem_1.1.0          yaml_2.3.12           otel_0.2.0           
#> [28] tools_4.5.2           memoise_2.0.1         checkmate_2.3.3      
#> [31] dplyr_1.1.4           fastmatch_1.1-8       vctrs_0.7.1          
#> [34] R6_2.6.1              lifecycle_1.0.5       fs_1.6.6             
#> [37] stringfish_0.18.0     htmlwidgets_1.6.4     ragg_1.5.0           
#> [40] PreciseSums_0.7       pkgconfig_2.0.3       desc_1.4.3           
#> [43] rex_1.2.1             pkgdown_2.2.0         RcppParallel_5.1.11-1
#> [46] bslib_0.9.0           pillar_1.11.1         gtable_0.3.6         
#> [49] glue_1.8.0            Rcpp_1.1.1            systemfonts_1.3.1    
#> [52] xfun_0.56             tibble_3.3.1          tidyselect_1.2.1     
#> [55] sys_3.4.3             knitr_1.51            farver_2.1.2         
#> [58] dparser_1.3.1-13      htmltools_0.5.9       nlme_3.1-168         
#> [61] labeling_0.4.3        rmarkdown_2.30        compiler_4.5.2       
#> [64] S7_0.2.1

Matthew Fidler

2026-01-27