rxode2 Transit Compartment Models

Savic 2008 first introduced the idea of transit compartments being a mechanistic explanation of a a lag-time type phenomena. rxode2 has special handling of these models:

You can specify this in a similar manner as the original paper. Note that we use evid=7 instead of evid=1 for these sorts of transit compartment models. evid=7 is the transit compartment model/phantom event. This puts the dose in the dose() function and calculates time since last dose tad() but doesn’t actually put the dose in the compartment. This allows the transit() function to easily apply to the compartment.

library(rxode2)

## rxode2 3.0.4.9000 using 2 threads (see ?getRxThreads)
##   no cache: create with `rxCreateCache()`

mod <- function() {
  model({
    ## Table 3 from Savic 2007
    cl = 17.2 # (L/hr)
    vc = 45.1 # L
    ka = 0.38 # 1/hr
    mtt = 0.37 # hr
    bio=1
    n = 20.1
    k = cl/vc
    ktr = (n+1)/mtt
    ## note that lgammafn is the same as lgamma in R.
    d/dt(depot) = exp(log(bio*podo(depot))+log(ktr)+n*log(ktr*tad(depot))-
                        ktr*tad(depot)-lgammafn(n+1))-ka*depot
    d/dt(cen) = ka*depot-k*cen
  })
}

et <- et(0, 7, length.out=200) %>%
  et(amt=20, time=0, evid=7)

transit <- rxSolve(mod, et)

## i parameter labels from comments are typically ignored in non-interactive mode

## i Need to run with the source intact to parse comments

## using C compiler: ‘gcc (Ubuntu 13.3.0-6ubuntu2~24.04) 13.3.0’

plot(transit, cen, ylab="Central Concentration")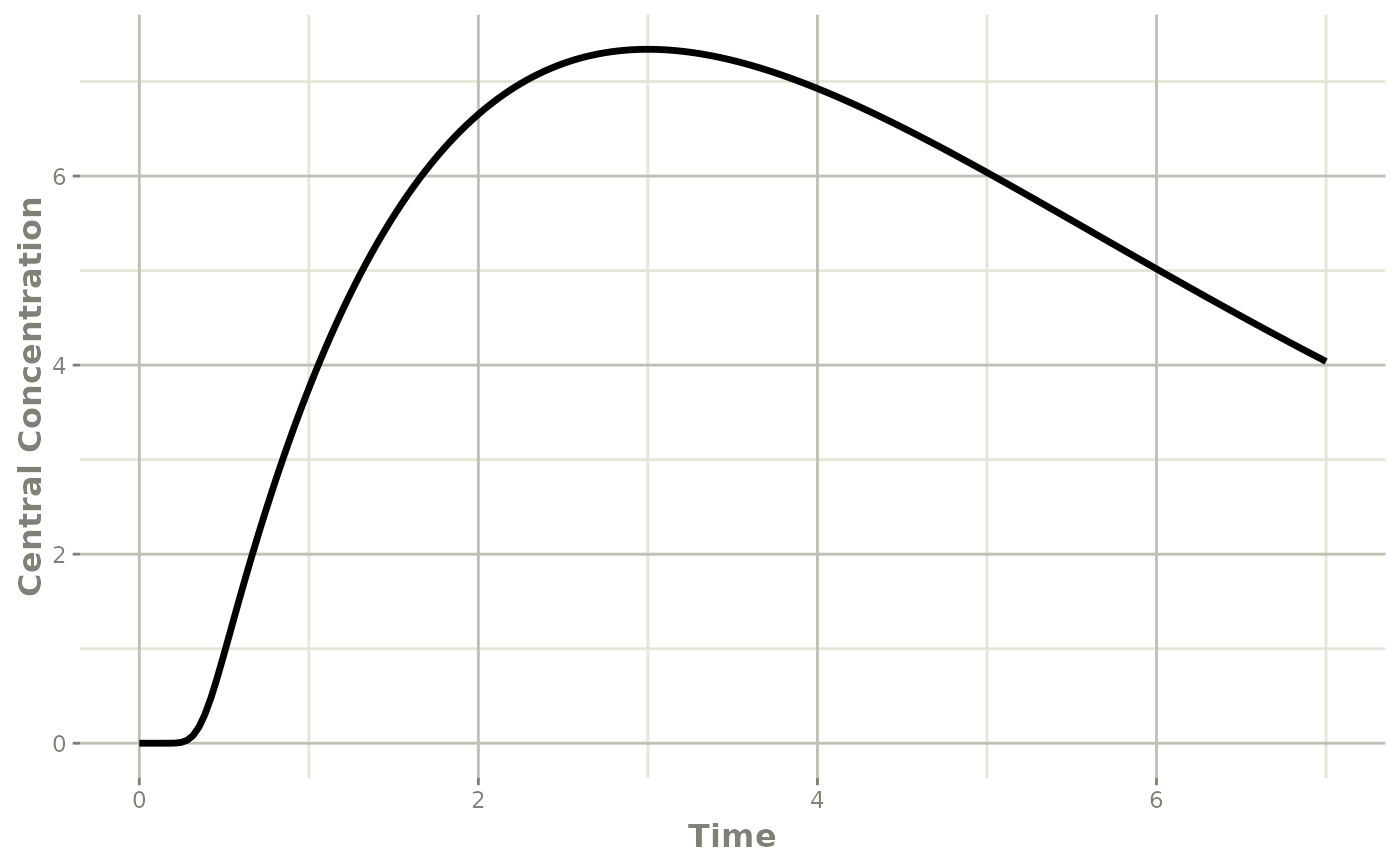

Another option is to specify the transit compartment function transit syntax. This specifies the parameters transit(number of transit compartments, mean transit time, bioavailability). The bioavailability term is optional.

The same model can be specified by:

mod <- function() {
  ini({
    ## Table 3 from Savic 2007
    cl  <- 17.2 # (L/hr)
    vc  <- 45.1 # L
    ka  <- 0.38 # 1/hr
    mtt <- 0.37 # hr
    bio <- 1
    n   <- 20.1
  })
  model({
    k           <- cl/vc
    ktr         <- (n+1)/mtt
    d/dt(depot) <- transit(n,mtt,bio)-ka*depot
    d/dt(cen)   <- ka*depot-k*cen
  })
}

et <- et(0, 7, length.out=200) %>%
  et(amt=20, evid=7)

transit <- rxSolve(mod, et)

## i parameter labels from comments are typically ignored in non-interactive mode

## i Need to run with the source intact to parse comments

## using C compiler: ‘gcc (Ubuntu 13.3.0-6ubuntu2~24.04) 13.3.0’

plot(transit, cen, ylab="Central Concentration")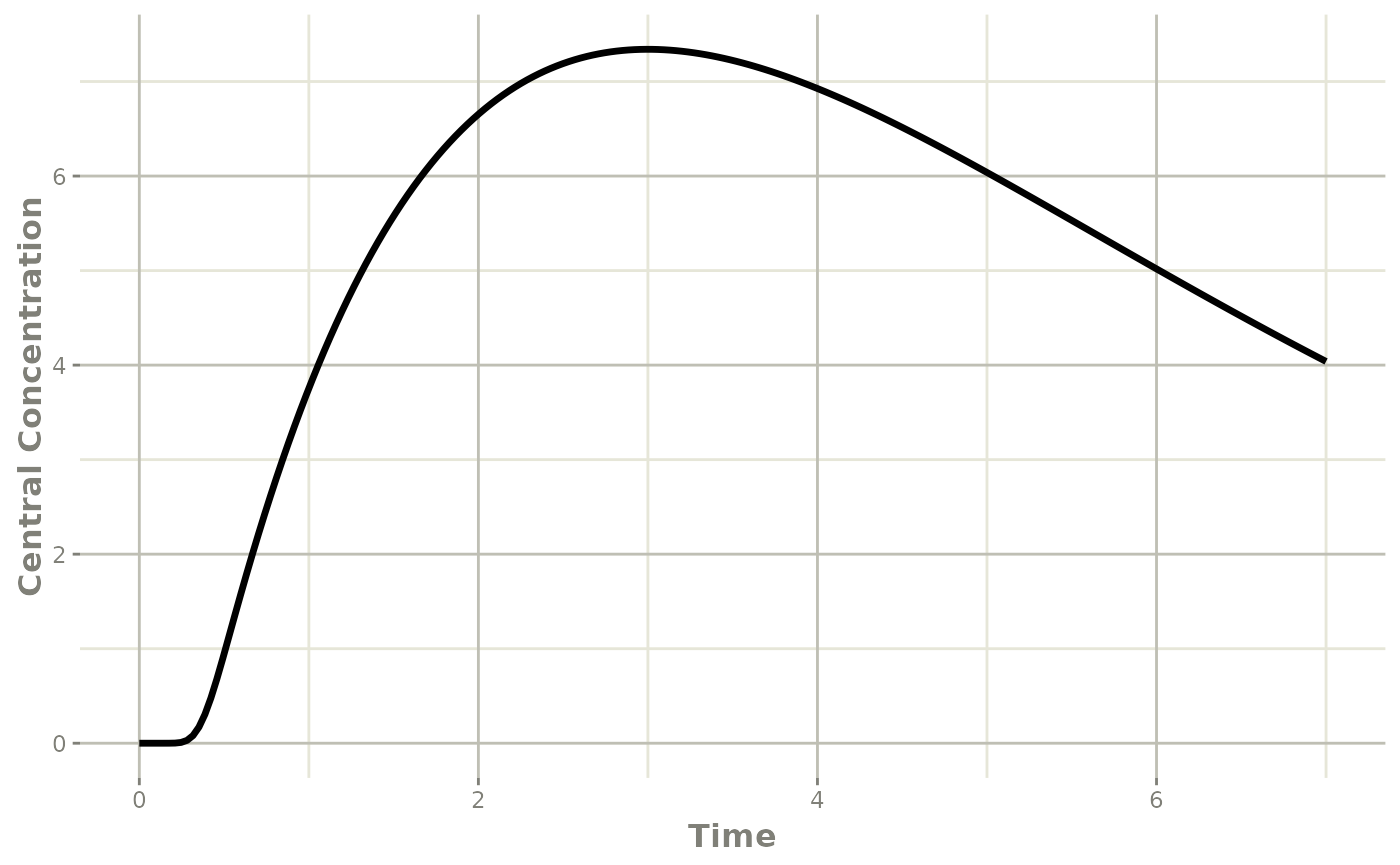

A couple of things to keep in mind when using this approach:

This approach implicitly assumes that the absorption through the transit compartment is completed before the next dose begins
Different types of doses (ie bolus/infusion) to the compartment affect the time after dose calculation (tad) which is used in the transit compartment calculation. These (therefore) are not currently supported. The most stable way is to use tad(cmt) and podo(cmt), this way doses to other compartments do not affect the transit compartment calculation.
Internally, the transit syntax uses either the currently defined cmt d/dt(cmt)=transit(...), or cmt. If the transit compartment is used outside of a d/dt() (not recommended), the cmt that is used is the last d/dt(cmt) defined it the model. This also means compartments do not affect one another (ie a oral, transit compartment drug dosed immediately with an IV infusion)

2025-04-29