Using rxode2 data frames
Creating an interactive data frame
rxode2 supports returning a solved object that is a
modified data-frame. This is done by the predict(),
solve(), or rxSolve() methods.
library(rxode2)
library(units)
## Setup example model
mod1 <- function() {
ini({
# central
KA <- 2.94E-01
CL <- 1.86E+01
# peripheral
V2 <- 4.02E+01
Q <- 1.05E+01
V3 <- 2.97E+02
# effects
Kin <- 1
Kout <- 1
EC50 <- 200
})
model({
C2 <- centr/V2
C3 <- peri/V3
d/dt(depot) <- -KA*depot
d/dt(centr) <- KA*depot - CL*C2 - Q*C2 + Q*C3
d/dt(peri) <- Q*C2 - Q*C3
d/dt(eff) <- Kin - Kout*(1-C2/(EC50+C2))*eff
eff(0) <- 1
})
}
## Seup parameters and initial conditions
## Setup dosing event information
ev <- et(amountUnits="mg", timeUnits = "hours") |>
et(amt=10000, addl=9, ii=12) |>
et(amt=20000, addl=4, time=120, ii=24) |>
et(0:240)
## Now solve
x <- predict(mod1, ev)
x
#> -- Solved rxode2 object --
#> -- Parameters (x$params): --
#> KA CL V2 Q V3 Kin Kout EC50
#> 0.294 18.600 40.200 10.500 297.000 1.000 1.000 200.000
#> -- Initial Conditions (x$inits): --
#> depot centr peri eff
#> 0 0 0 1
#> -- First part of data (object): --
#> # A tibble: 241 x 7
#> time C2 C3 depot centr peri eff
#> [h] <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 0 0 0 10000 0 0 1
#> 2 1 44.4 0.920 7453. 1784. 273. 1.08
#> 3 2 54.9 2.67 5554. 2206. 794. 1.18
#> 4 3 51.9 4.46 4140. 2087. 1324. 1.23
#> 5 4 44.5 5.98 3085. 1789. 1776. 1.23
#> 6 5 36.5 7.18 2299. 1467. 2132. 1.21
#> # i 235 more rowsUsing the solved object as a simple data frame
The solved object acts as a data.frame or
tbl that can be filtered by dpylr. For example
you could filter it easily.
library(dplyr)
## You can drop units for comparisons and filtering
x <- mod1 |> solve(ev) |>
drop_units() |> filter(time <= 3) |> as_tibble()
## or keep them and compare with the proper units.
x <- mod1 |> solve(ev) |>
filter(time <= set_units(3, hr)) |> as_tibble()
x
#> # A tibble: 4 x 7
#> time C2 C3 depot centr peri eff
#> [h] <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 0 0 0 10000 0 0 1
#> 2 1 44.4 0.920 7453. 1784. 273. 1.08
#> 3 2 54.9 2.67 5554. 2206. 794. 1.18
#> 4 3 51.9 4.46 4140. 2087. 1324. 1.23Updating the data-set interactively
However it isn’t just a simple data object. You can use the solved object to update parameters on the fly, or even change the sampling time.
First we need to recreate the original solved system:
x <- mod1 |> solve(ev)
print(x)
#> -- Solved rxode2 object --
#> -- Parameters ($params): --
#> KA CL V2 Q V3 Kin Kout EC50
#> 0.294 18.600 40.200 10.500 297.000 1.000 1.000 200.000
#> -- Initial Conditions ($inits): --
#> depot centr peri eff
#> 0 0 0 1
#> -- First part of data (object): --
#> # A tibble: 241 x 7
#> time C2 C3 depot centr peri eff
#> [h] <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 0 0 0 10000 0 0 1
#> 2 1 44.4 0.920 7453. 1784. 273. 1.08
#> 3 2 54.9 2.67 5554. 2206. 794. 1.18
#> 4 3 51.9 4.46 4140. 2087. 1324. 1.23
#> 5 4 44.5 5.98 3085. 1789. 1776. 1.23
#> 6 5 36.5 7.18 2299. 1467. 2132. 1.21
#> # i 235 more rowsModifying observation times for rxode2
Notice that the initial effect is now 2.
You can also change the sampling times easily by this method by
changing t or time. For example:
x$t <- seq(0,5,length.out=20)
print(x)
#> -- Solved rxode2 object --
#> -- Parameters ($params): --
#> KA CL V2 Q V3 Kin Kout EC50
#> 0.294 18.600 40.200 10.500 297.000 1.000 1.000 200.000
#> -- Initial Conditions ($inits): --
#> depot centr peri eff
#> 0 0 0 1
#> -- First part of data (object): --
#> # A tibble: 20 x 7
#> time C2 C3 depot centr peri eff
#> [h] <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 0 0 0 10000 0 0 1
#> 2 0.263 16.8 0.0817 9255. 677. 24.3 1.01
#> 3 0.526 29.5 0.299 8566. 1187. 88.7 1.03
#> 4 0.789 38.9 0.615 7929. 1562. 183. 1.06
#> 5 1.05 45.5 1.00 7338. 1830. 298. 1.09
#> 6 1.32 50.1 1.44 6792. 2013. 427. 1.12
#> # i 14 more rows
plot(x)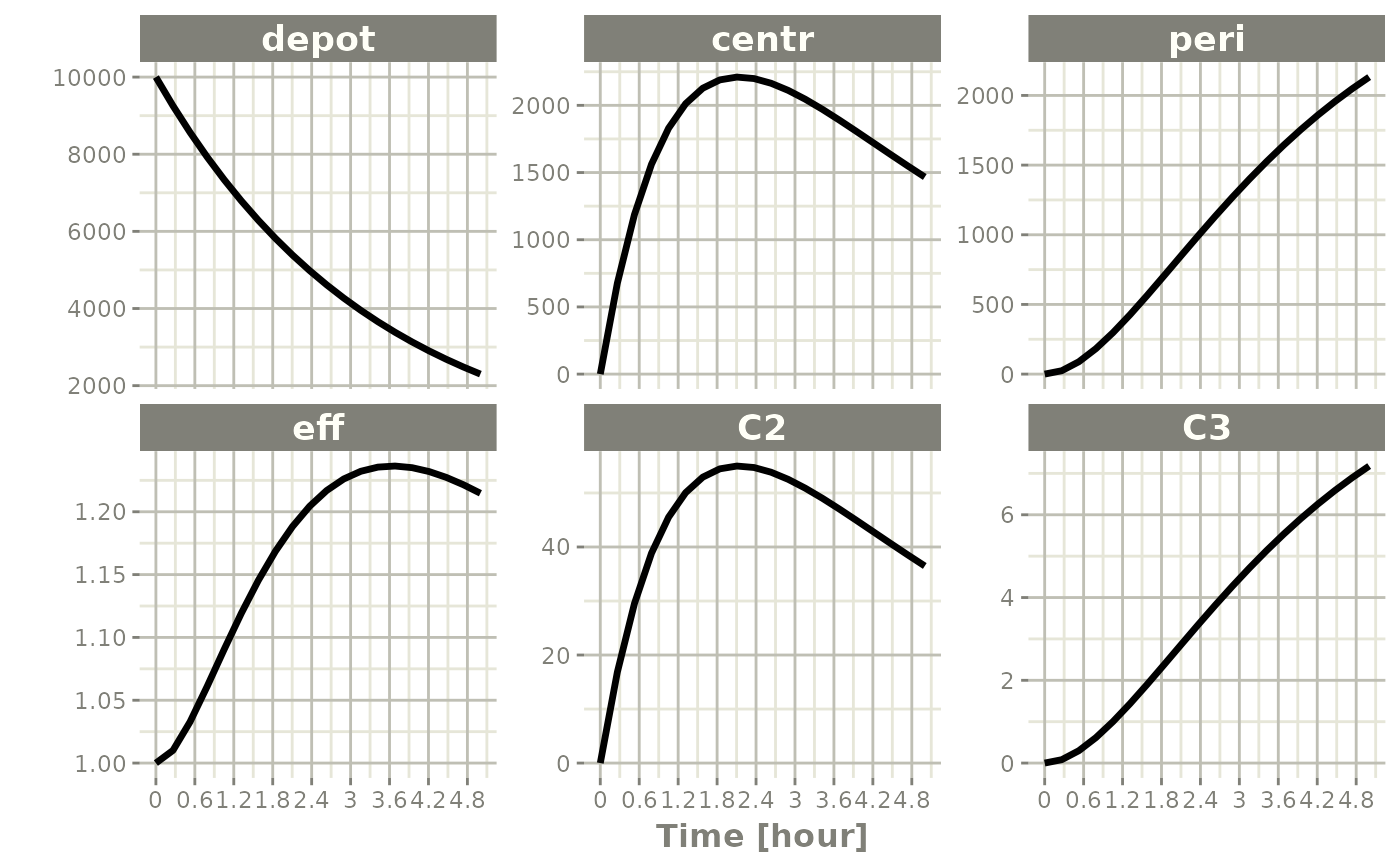
Modifying simulation parameters
You can also access or change parameters by the $
operator. For example, accessing KA can be done by:
x$KA
#> [1] 0.294And you may change it by assigning it to a new value.
x$KA <- 1
print(x)
#> -- Solved rxode2 object --
#> -- Parameters ($params): --
#> KA CL V2 Q V3 Kin Kout EC50
#> 1.0 18.6 40.2 10.5 297.0 1.0 1.0 200.0
#> -- Initial Conditions ($inits): --
#> depot centr peri eff
#> 0 0 0 1
#> -- First part of data (object): --
#> # A tibble: 20 x 7
#> time C2 C3 depot centr peri eff
#> [h] <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 0 0 0 10000 0 0 1
#> 2 0.263 52.2 0.261 7686. 2098. 77.6 1.03
#> 3 0.526 83.3 0.900 5908. 3348. 267. 1.09
#> 4 0.789 99.8 1.75 4541. 4010. 519. 1.15
#> 5 1.05 106. 2.69 3490. 4273. 800. 1.21
#> 6 1.32 106. 3.66 2683. 4272. 1086. 1.26
#> # i 14 more rows
plot(x)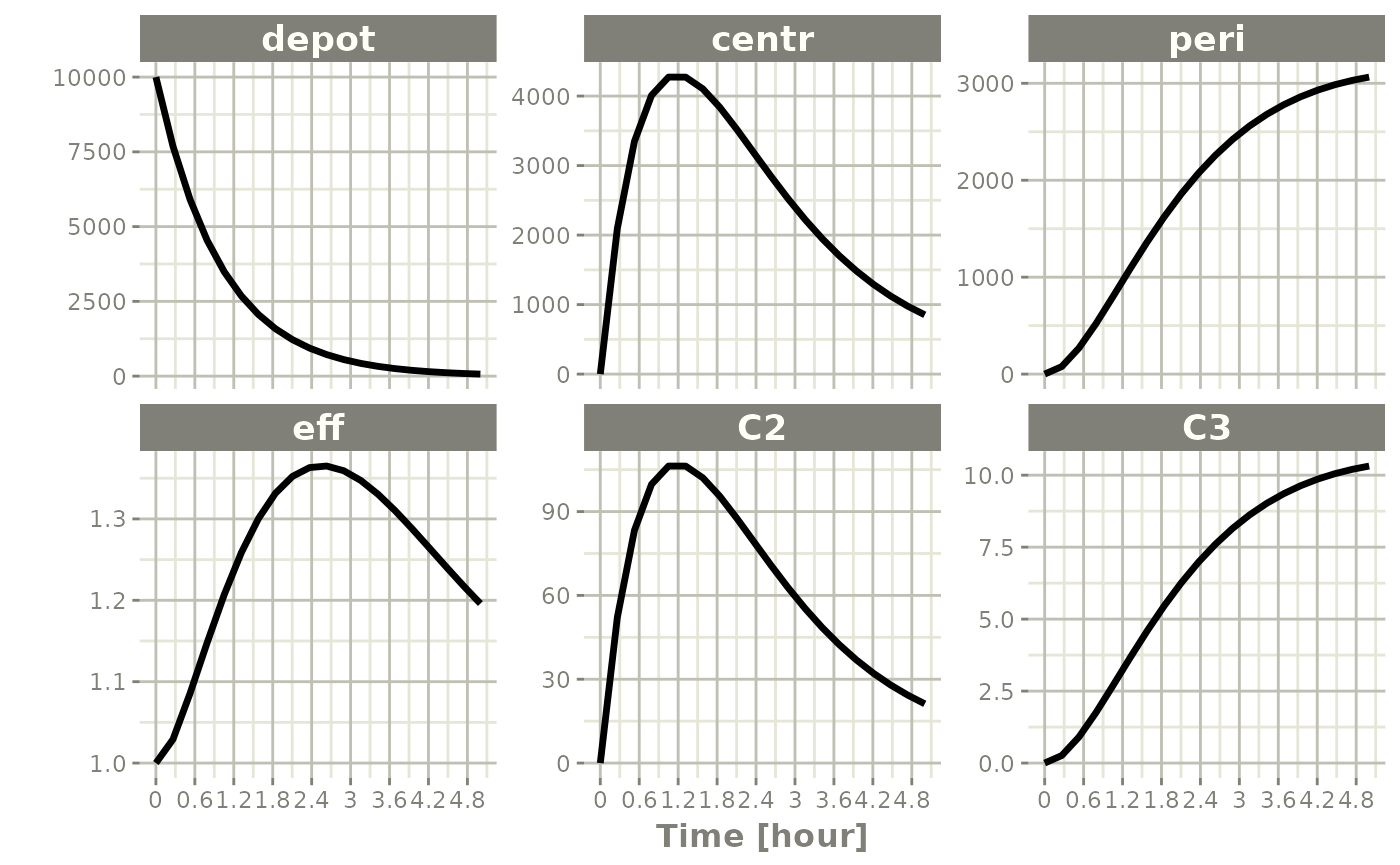
You can access/change all the parameters, initialization(s) or events
with the $params, $inits, $events
accessor syntax, similar to what is used above.
This syntax makes it easy to update and explore the effect of various parameters on the solved object.
