Simulate using Parameter Uncertainty
Source:vignettes/articles/simulate-uncertainty.Rmd
simulate-uncertainty.RmdThis page shows a simple work-flow for directly simulating a different dosing paradigm than what was modeled taking into account the modeled uncertainty. This workflow is very similar to simply simulating without uncertainty in the parameters themselves.
Step 1: Import the model
library(monolix2rx)
library(rxode2)
# its best practice to set the seed for the simulations
set.seed(42)
rxSetSeed(42)
# You use the path to the monolix mlxtran file
# In this case we will us the theophylline project included in monolix2rx
pkgTheo <- system.file("theo/theophylline_project.mlxtran", package="monolix2rx")
# Note you have to setup monolix2rx to use the model library or save
# the model as a separate file
mod <- monolix2rx(pkgTheo)
#> ℹ integrated model file 'oral1_1cpt_kaVCl.txt' into mlxtran object
#> ℹ updating model values to final parameter estimates
#> ℹ done
#> ℹ reading run info (# obs, doses, Monolix Version, etc) from summary.txt
#> ℹ done
#> ℹ reading covariance from FisherInformation/covarianceEstimatesLin.txt
#> ℹ done
#> Warning in .dataRenameFromMlxtran(data, .mlxtran): NAs introduced by coercion
#> ℹ imported monolix and translated to rxode2 compatible data ($monolixData)
#> ℹ imported monolix ETAS (_SAEM) imported to rxode2 compatible data ($etaData)
#> ℹ imported monolix pred/ipred data to compare ($predIpredData)
#> ℹ solving ipred problem
#> ℹ done
#> ℹ solving pred problem
#> ℹ done
print(mod)
#> ── rxode2-based free-form 2-cmt ODE model ──────────────────────────────────────
#> ── Initalization: ──
#> Fixed Effects ($theta):
#> ka_pop V_pop Cl_pop a b
#> 0.42699448 -0.78635157 -3.21457598 0.43327956 0.05425953
#>
#> Omega ($omega):
#> omega_ka omega_V omega_Cl
#> omega_ka 0.4503145 0.00000000 0.00000000
#> omega_V 0.0000000 0.01594701 0.00000000
#> omega_Cl 0.0000000 0.00000000 0.07323701
#>
#> States ($state or $stateDf):
#> Compartment Number Compartment Name
#> 1 1 depot
#> 2 2 central
#> ── μ-referencing ($muRefTable): ──
#> theta eta level
#> 1 ka_pop omega_ka id
#> 2 V_pop omega_V id
#> 3 Cl_pop omega_Cl id
#>
#> ── Model (Normalized Syntax): ──
#> function() {
#> description <- "The administration is extravascular with a first order absorption (rate constant ka).\nThe PK model has one compartment (volume V) and a linear elimination (clearance Cl).\nThis has been modified so that it will run without the model library"
#> dfObs <- 120
#> dfSub <- 12
#> thetaMat <- lotri({
#> ka_pop ~ 0.09785
#> V_pop ~ c(0.00082606, 0.00041937)
#> Cl_pop ~ c(-4.2833e-05, -6.7957e-06, 1.1318e-05)
#> omega_ka ~ c(omega_ka = 0.022259)
#> omega_V ~ c(omega_ka = -7.6443e-05, omega_V = 0.0014578)
#> omega_Cl ~ c(omega_ka = 3.062e-06, omega_V = -1.2912e-05,
#> omega_Cl = 0.0039578)
#> a ~ c(omega_ka = -0.0001227, omega_V = -6.5914e-05, omega_Cl = -0.00041194,
#> a = 0.015333)
#> b ~ c(omega_ka = -1.3886e-05, omega_V = -3.1105e-05,
#> omega_Cl = 5.2805e-05, a = -0.0026458, b = 0.00056232)
#> })
#> validation <- c("ipred relative difference compared to Monolix ipred: 0.04%; 95% percentile: (0%,0.52%); rtol=0.00038",
#> "ipred absolute difference compared to Monolix ipred: 95% percentile: (0.000362, 0.00848); atol=0.00254",
#> "pred relative difference compared to Monolix pred: 0%; 95% percentile: (0%,0%); rtol=6.6e-07",
#> "pred absolute difference compared to Monolix pred: 95% percentile: (1.6e-07, 1.27e-05); atol=3.66e-06",
#> "iwres relative difference compared to Monolix iwres: 0%; 95% percentile: (0.06%,32.22%); rtol=0.0153",
#> "iwres absolute difference compared to Monolix pred: 95% percentile: (0.000403, 0.0138); atol=0.00305")
#> ini({
#> ka_pop <- 0.426994483535611
#> V_pop <- -0.786351566327091
#> Cl_pop <- -3.21457597916301
#> a <- c(0, 0.433279557549051)
#> b <- c(0, 0.0542595276206251)
#> omega_ka ~ 0.450314511978718
#> omega_V ~ 0.0159470121255372
#> omega_Cl ~ 0.0732370098834837
#> })
#> model({
#> cmt(depot)
#> cmt(central)
#> ka <- exp(ka_pop + omega_ka)
#> V <- exp(V_pop + omega_V)
#> Cl <- exp(Cl_pop + omega_Cl)
#> d/dt(depot) <- -ka * depot
#> d/dt(central) <- +ka * depot - Cl/V * central
#> Cc <- central/V
#> CONC <- Cc
#> CONC ~ add(a) + prop(b) + combined1()
#> })
#> }Step 2: Look at a different dosing paradigm
Lets say that in this case instead of a single dose, we want to see what the concentration profile is with a single day of BID dosing. In this case is done by creating a quick event table.
Step 3: Solve using the uncertainty in the NONMEM model
To use the uncertainty in the model, it is a simple matter of telling
how many times rxode2() should sample with
nStud=X. In this case we will use 100.
s <- rxSolve(mod, ev, nStud=100)
#> ℹ using locf interpolation like Monolix, specify directly to change
#> ℹ using dfSub=12 from Monolix
#> ℹ using dfObs=120 from Monolix
#> ℹ using thetaMat from Monolix
#> ℹ using Monolix specified atol=1e-06
#> ℹ using Monolix specified rtol=1e-06
#> ℹ Since Monolix doesn't use ssRtol, set ssRtol=100
#> ℹ Since Monolix doesn't use ssRtol, set ssAtol=100
#> ℹ Since Monolix uses a set number of doses for steady state use maxSS=8, minSS=7
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
s
#> ── Solved rxode2 object ──
#> ── Parameters (x$params): ──
#> # A tibble: 10,000 × 10
#> sim.id id ka_pop V_pop Cl_pop a b omega_ka omega_V omega_Cl
#> <int> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 1 1 0.281 -0.770 -3.22 0.475 0.0653 0.470 -0.208 0.483
#> 2 1 2 0.281 -0.770 -3.22 0.475 0.0653 0.654 0.0861 0.129
#> 3 1 3 0.281 -0.770 -3.22 0.475 0.0653 -0.0747 0.168 0.500
#> 4 1 4 0.281 -0.770 -3.22 0.475 0.0653 0.126 -0.0226 0.479
#> 5 1 5 0.281 -0.770 -3.22 0.475 0.0653 -0.162 0.000264 -0.205
#> 6 1 6 0.281 -0.770 -3.22 0.475 0.0653 -1.13 -0.239 0.0941
#> 7 1 7 0.281 -0.770 -3.22 0.475 0.0653 -0.335 0.0134 0.00490
#> 8 1 8 0.281 -0.770 -3.22 0.475 0.0653 -0.869 -0.239 0.000511
#> 9 1 9 0.281 -0.770 -3.22 0.475 0.0653 1.35 -0.122 0.667
#> 10 1 10 0.281 -0.770 -3.22 0.475 0.0653 0.314 0.0494 -0.552
#> # ℹ 9,990 more rows
#> ── Initial Conditions (x$inits): ──
#> depot central
#> 0 0
#>
#> Simulation with uncertainty in:
#> • parameters (x$thetaMat for changes)
#> • omega matrix (x$omegaList)
#> • sigma matrix (x$sigmaList)
#>
#> ── First part of data (object): ──
#> # A tibble: 150,000 × 12
#> sim.id id time ka V Cl Cc CONC ipredSim sim depot
#> <int> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 1 1 1 2.12 0.376 0.0646 8.36 8.36 8.36 8.50 0.481
#> 2 1 1 2 2.12 0.376 0.0646 8.04 8.04 8.04 9.71 0.0577
#> 3 1 1 3 2.12 0.376 0.0646 6.90 6.90 6.90 7.77 0.00694
#> 4 1 1 4 2.12 0.376 0.0646 5.82 5.82 5.82 5.07 0.000833
#> 5 1 1 5 2.12 0.376 0.0646 4.91 4.91 4.91 4.91 0.000100
#> 6 1 1 6 2.12 0.376 0.0646 4.13 4.13 4.13 3.79 0.0000121
#> # ℹ 149,994 more rows
#> # ℹ 1 more variable: central <dbl>Step 4: Summarize and plot
Since there is a bunch of data, a confidence band of the simulation with uncertainty would be helpful.
One way to do that is to select the interesting components, create a confidence interval and then plot the confidence bands:
sci <- confint(s, parm=c("CONC", "sim"))
#> summarizing data...done
sci
#> # A tibble: 90 × 7
#> p1 time trt p2.5 p50 p97.5 Percentile
#> <dbl> <dbl> <fct> <dbl> <dbl> <dbl> <fct>
#> 1 0.0250 1 CONC 0.741 2.40 4.39 2.5%
#> 2 0.5 1 CONC 4.21 6.21 7.25 50%
#> 3 0.975 1 CONC 7.89 9.32 11.1 97.5%
#> 4 0.0250 2 CONC 1.33 3.80 5.59 2.5%
#> 5 0.5 2 CONC 5.76 6.94 7.45 50%
#> 6 0.975 2 CONC 8.22 9.14 10.6 97.5%
#> 7 0.0250 3 CONC 1.79 4.36 5.42 2.5%
#> 8 0.5 3 CONC 6.04 6.66 7.05 50%
#> 9 0.975 3 CONC 7.79 8.71 9.99 97.5%
#> 10 0.0250 4 CONC 2.12 4.36 5.26 2.5%
#> # ℹ 80 more rows
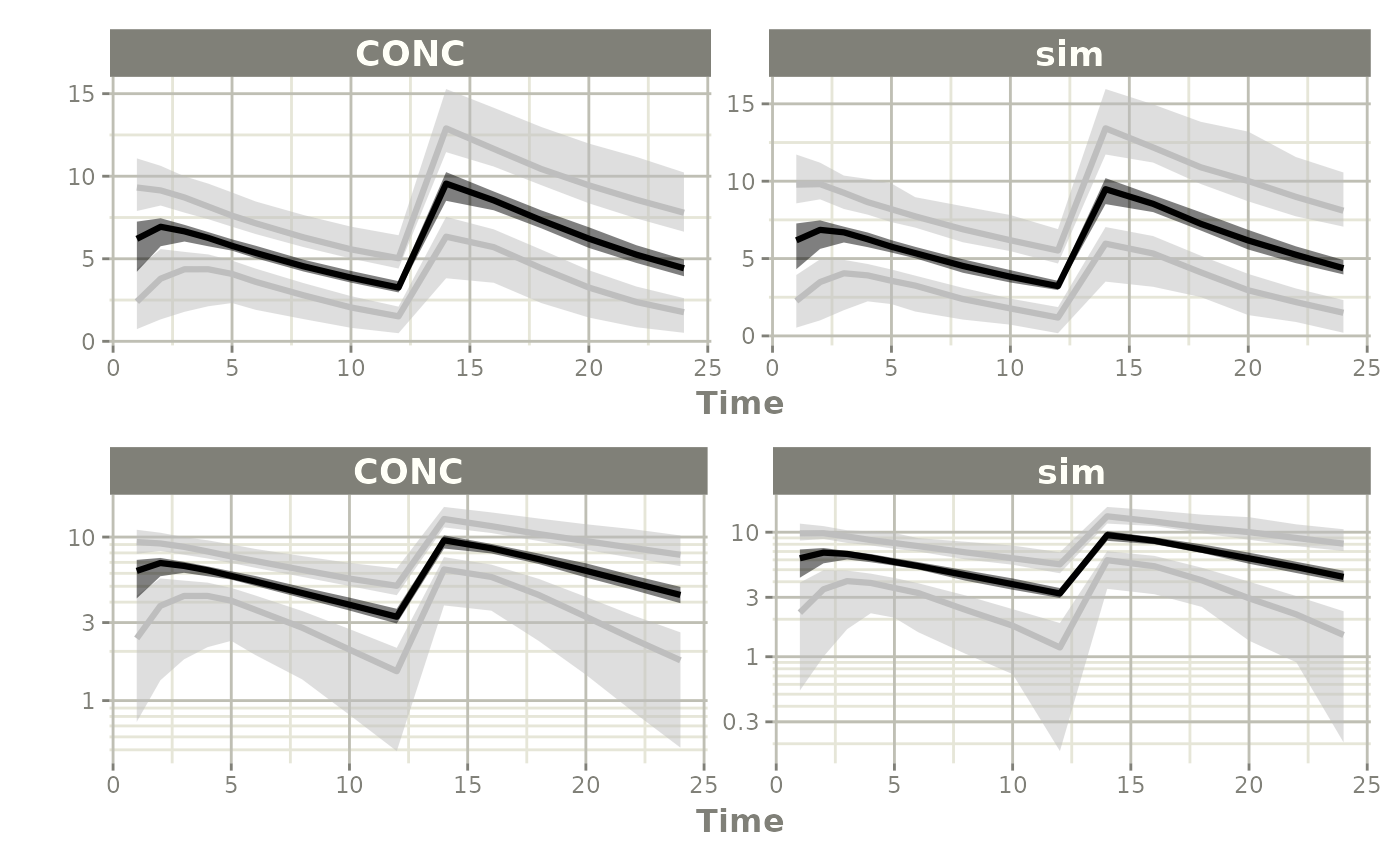
p1 <- plot(sci)
p2 <- plot(sci, log="y")
library(patchwork)
p1/p2